Introduction
As an interdisciplinary artist delving into the intricacies of perspective, I stumbled upon a fascinating intersection of art and science. I was experimenting with known transformations of flat points into curved spaces and saw intriguing patterns emerging within the evolving, embedded geometry.
What initially seemed like a coincidence soon revealed a striking alignment with the principles of electromagnetism, a major fundamental force in the universe. This is a topic that normal civilian researchers don’t academically have access to and my biggest hurdle has been publication and finding those who are willing to test it.

It was only after years of work to fine tune the sequence that a self-evident, geometric primer appeared, along with a launch sequence that boots up a universe. This is an outlandish claim from someone not holding several PhDs and a parking pass a CERN but the evidence speaks for itself. Learning the sequence is not hard being under a fourth grade level, but all the pieces make it heavier and a primer is almost required to help keep things organized.
Over the next following pages, I will explain the origins of each of the 22 geometric objects in my geometric primer for electromagnetism that make up the first illustration. Of these 22 objects, 18 of these were extracted together from a known six-point perspective system, creating three similar geometric sequences (Six Points x Three Versions = 18 Geometries). This step is absolutely in the wheelhouse of someone with a BA degree in interdisciplinary arts and science which I happen to have. I did start my journey totally in my lane but it was this set of geometries that I saw aligned with the first ever image of a photon, a repeatable step. This might scare the civilian or cause researchers to royally scoff, but my geometric primer is elementary, elegant, and accessibility, opening up the realm of science to whole new generation of explorers.
To start that journey, it is best to follow my path up the mountain and gain a new perspective on the topic of, well, perspective. After gaining perspective, you will understand the origins of my base geometries and have enough information to look for an alignment yourself.
Evolving Perspective
MC Escher is a famous painter of perspective and it is said that his torch was passed to Richard “Dick” Termes who outlined his method in 1997 for painting a curved picture on a curved surface, specifically, a sphere. Termes, celebrated for his ability to breathe life onto spherical canvases, transcends the traditional artistic realm of flat canvases or flat walls or even 3-D sculptures. His masterpieces, proudly displayed in museums, reach beyond the confines of gallery walls and take the viewer on a journey inside his images. Notably, his 2002 creation, “Big Bang,” graced the cover of a French edition of Stephen Hawking’s monumental work, “The Brief History of Time.”
In the turbulent 1960s, Termes took on a profound challenge: to elevate the principles of flat perspective with only three vanishing points and “incorporate the whole world around us.” This ambitious exploration propelled him beyond modern limitations evolving a complete series of perspective, starting from a single vanishing point and evolving all the way up to six.
Wait, you might say, Termes just outlined a new way to paint on globes, right? Not quite. When you look at globe, you are seeing a flat image on a curved surface. Termes’ paints a curved imaged on a curved object, a method which tricks a human’s visual perception into thinking they are seeing inside the sphere. His overarching goal was to achieve such a level of realism that the viewer would be immersed in the illusion of standing within the sphere gazing outward into an expansive reality. It is easy to understand why Termes is a worthy legacy to optical illusion master MC Escher, as a Termesphere is a marvelous optical illusion and also happens to be based in solid mathematics.
Attaining six vanishing points demanded a mastery of artistic accuracy and, of course, five other underlying perspectives. As a student of the arts, this is why I had been studying the topic and delved so deeply. Perspective is important to artists and is a great way to understand art in general. How mature is an artist, art style, or even an art movement? Well, you can compare the their relative perspective styles, dear Watson.
I was curious about the transformations that were occurring within Termes’ strict evolutionary process because I didn’t understand why they were happening. We have straight lines and then we have curved lines. I was losing the pattern so I studied each perspective and first saw the Euclid geometries of a point, line, and vector, an almost natural progression. I began to copy these into my personal study and by the time I was done, the result was 18 geometries. This sketch then sat on a shelf until I was needing a framework for a geometric boot sequence and remembered; I already had one. That is jumping ahead. I feel obliged to review the full system of perspective and my extraction method further.
The subsequent discussion below provides a short overview of perspective, starting with a zero point before segue-way’ing into historic three-points, followed by a delve into the last three vanishing points outlined by Termes. With the main bulk of the geometries established, I can introduce Electromagnetism with the first ever published image taken of the wave-particle duality of light in the next part. This image of a photon is simply placed at the end of Row One from my extracted Geometries – nothing else.
To me, these 19 objects together strongly teased at a question: How geometric was our universe? No, like really HOW geometric was it? If it was extremely geometric, I would have not just discovered something but rather, have uncovered a secret to the universe – hiding in plain sight.
Zero-Point Perspective
The principles of perspective in art aren’t universally fixed and are influenced by cultural tradition, time periods, technology, access, etc. The basic concept of zero-point perspective comes in many varieties and is a technical skill that is hard to achieve. Zero-point might seem to be a perspective about “nothing” but rather, it’s a way of capturing the concept of chaos.
True chaos is hard to achieve, even by computers which for instance, can’t just invent random numbers and therefore needed an entire industry based solely around this short coming known as Security. Anything created by a computer program is locked by the limitation of the parts of the program.
An iconic achievement in zero-point perspective is found in Jackson Pollock‘s splash paintings, notorious for their complexity and difficulty to replicate, especially without the influence of alcohol. Artists like Picasso took a different approach on perspective, deliberately deconstructing or exaggerating perspective with flatness, as seen in his cubism and multi-faceted faces. A famous example is Picasso’s series of The Bull where he slowly desolves the perspective of Le Taurea.

The takeaways for zero-point is that it absolutely exists and while it is without perspective, it is not without existence. This is identical logic to Geogr Cantor’s Empty Set which has an Absolute Value of one because it does exist; but, a Total Value of zero, because it is empty. Zero-Point perspective may also be an Empty Perspective. Regardles if you have an empty set, empty perspective, or maybe an empty dimension – all would be theoretical constructs that would allow for the evolution of any number of sets, perspectives, or dimensions. This means that one purpose of an empty [object] is as a natural foundation or canvas upon which other things may be evolved which gives us potential. Perspective, like dimensions or sets, can hold multiple meanings and all are correct within their proper context.
Classic Perspectives: One, Two, and Three Points
One-Point
Perspective

Has two sets of parallel lines, and a third set of lines disappearing into one vanishing point.
Two-Point
Perspective

Has one set of parallel lines, and the last two sets going off into two different vanishing points.
Three-Point
Perspective

(Missing Cube) Has three vanishing points and no parallel lines, with all lines radiating out on a flat plane.
So far, everything shown is very flat with regular angles. The first two perspectives are quite simple so I didn’t recreate all the graph lines because I was using a word processor and it’s tedious. By three-point perspective, I felt I couldn’t ignore graph lines any longer and the exercise helped me understand how Termes achieved Four-Point perspective so easily: he (said jokingly) cheated.
Four-Point Perspective
Again, there are a couple of different ways to achieve four vanishing points but it almost seems cheeky to just pop two copies of three-point perspective next to each other but it works. This process does start with six points and the moment the two equatorial (or mirrored) vanishing-points merge, curvature is achieved and we get four-vanishing points.

What this looks like in reality is called a fisheye lens effect because there is additional curvature being capture. For better visualization, here is an AI image of a person jumping into a pool, but frozen mid air showing the four points: the sun above, the water below, air to left and right. In the AI Photo, there are people standing around the pool, each rendered at different scales and almost looking bowed.
Another way to perceive four vanishing points was as a proto-cuboid and carrying it’s mass around the center.
Termes’ perspective system has gained some dimensionality or curvature but is still relatively flat so let us continue this journey.

Five-Point Perspective
Grid Lines
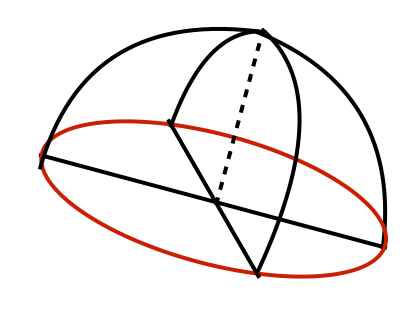
In four-point perspective we merged one set of grid lines and for the fifth-point, Termes merges the other remaining set of lines. This gives us a stereographic projection for half a sphere.
There is another way to experience this progression if that seemed a little disjointed to just say the other graph lines connect into a half-dome.
Another way I thought about the problem was with bubbles. One-point is one bubble, two-point is two bubbles, three-point is three bubbles, and four-point is four bubbles. With four bubbles, I had a four-chamber single bubble which could land on a surface to become a half-dome, still with four chambers. In a single step of internal movement, the fifth-point of perspective was created.
Several folks are able to see how to move from five-points into six without being told.
You can personally experience this perspective by laying on the ground and looking up at the ceiling or sky; if you are in a forest, up at the canopy of trees. Your body aligns with the cardinal directions (N, S, W, E) and above you is the fifth point.

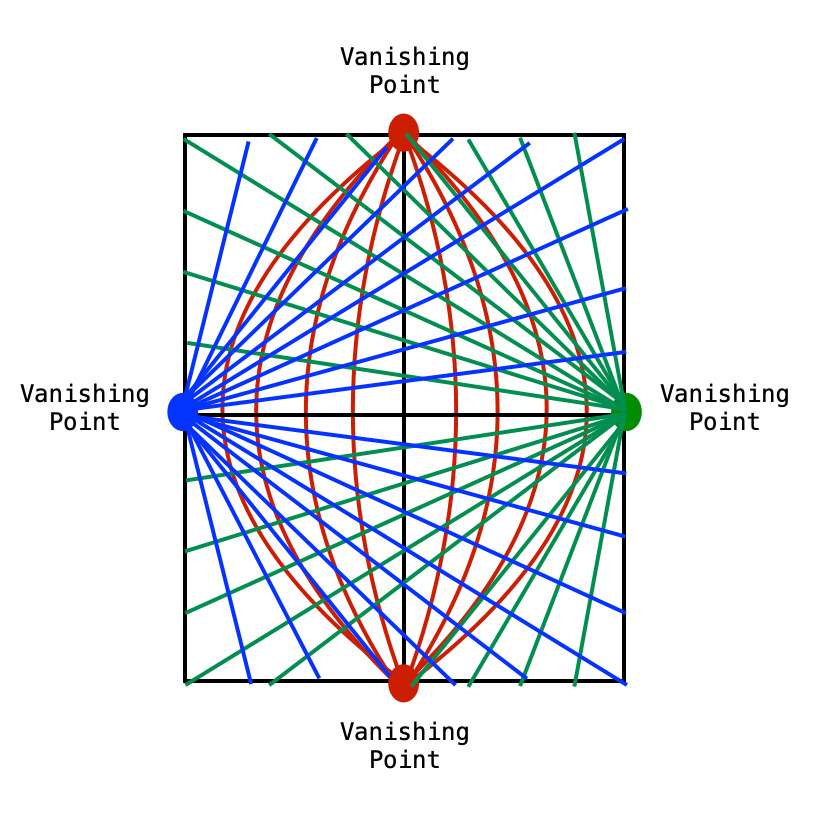
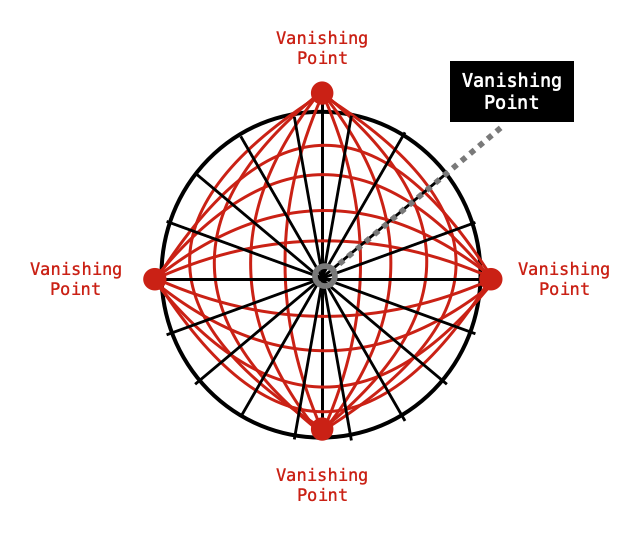
Six-Point Perspective
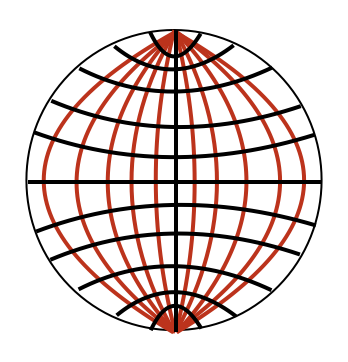
For Termes, his aim from the beginning was to map out grid lines for the surface of a sphere so an artist could follow them to accurately move from the realm of flat perspective into curved. Simply adding another half-dome gets us from five points to six! This act of geometric doubling keeps the sequence embedded, culminating in the exquisite balance and symmetry of a complete sphere.
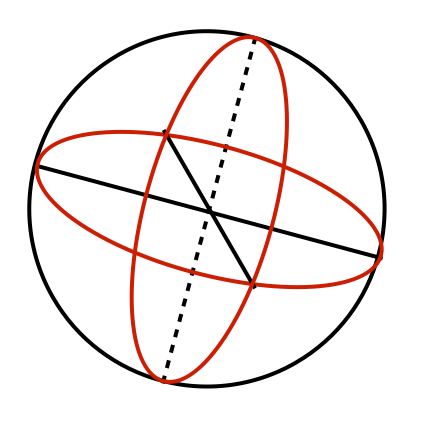
Flat and Curved Geometries
Termes achieved the mathematics needed for the grid lines that create a curved image on a curved surface and published his work in 1997. This is an example of true mastery of a craft, the intentional understanding and application of a process for a specific result. In this artistic alchemy, Termes triumphed in transmuting a sphere—a three-dimensional wonder—from the seemingly flat realms of logic.
It should NOT be surprising that anyone found Termes’ base geometries following an evolutionary journey from the flat realm into the curved.
Sandy’s Early Foundation: 18 Base Geometries
Thus you enter onto the scene of my early exploration into the world of flat and curved geometries.
Can you discern the subtleties within this collection—subatomic particles, forces, matter, and even the nuances of Electromagnetism? Neither did I, but I wasn’t looking.
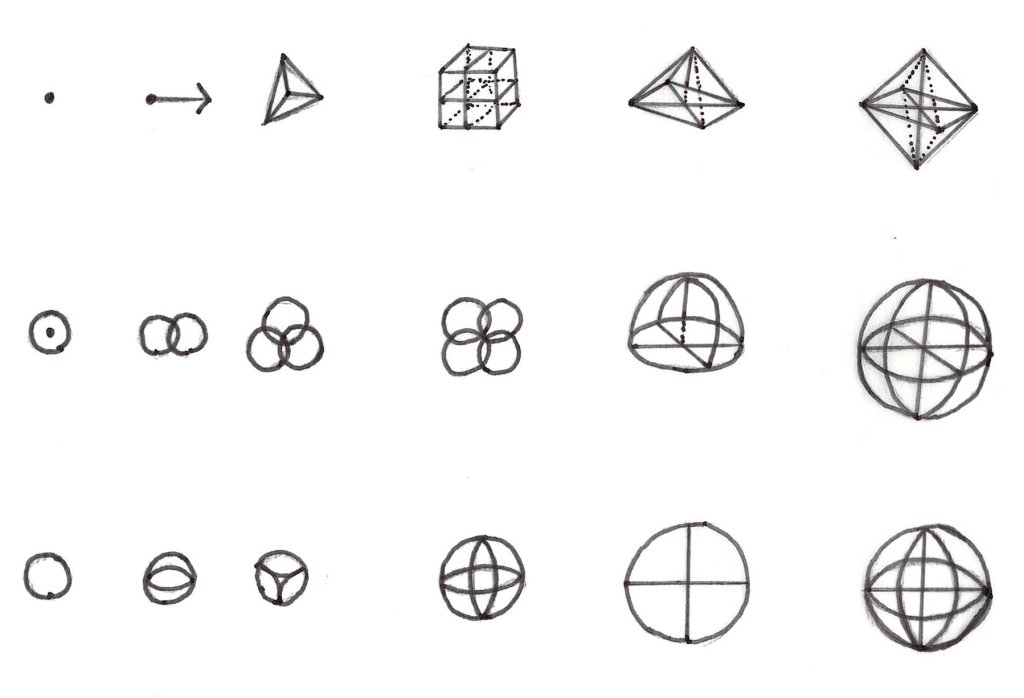
To start, Row 1 consisted of the Background geometries while Rows 2 and 3 consisted of the geometries for the foreground. I could have gone with a block point for Row 1 but did a round point; to match the style, I used a circle for the first objects in Rows 2 and 3. I kept all the geometries flat for Row 1 and decided for Rows 2 and 3 to do a side and top view of the same object. I arranged all the similar objects in columns for neatness and added a little space between Columns 3 and 4 because I sensed something was changing here.
Columns 1, 2 and 3 all contained what I considered to be different versions of points, rays, and vectors with different amounts of curvature. I realized Columns 4, 5, and 6 looked like major or complex versions of the same geometries. Crossing from Column 3 into Column 4 seemed to be causing a complexity event and the rules were being change. I personally wondered if there was another complexity event after column 6 or if all the rows could be connected together into a single sequence. The answer was: OMG!
ILLUSTRATIONS

ONE | The first step was a simple, singular object or point (L1). Which could be a point charged particle with any flavor, color, or charge.
GEOMETRIES


TWO | Next, the background points could be connected by a line segment or a ray (L2). The ray convey’s both external direction and potential.
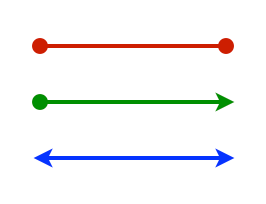

THREE | The third step was a field, magnitude or vector (L3) as it incorporates the x, y, and z coordinate system.


FOUR | The fourth step is a complex object resembling a cuboid (L4) but with no original parallel lines. A complex cuboid with parallel lines was used for simplicity sake and to represent the added depth.


FIVE | The fifth step is the development of a pole (L5) resulting from an internal movement that allows for energy efficiency. This might be called a complex, internal movement.


SIX | The sixth step is to double the fifth point creating a complex vector (L6) and a second opposite pole. It could also be drawn with the poles detached so it resembles an oscillating wave.
Granted, the above draft illustration might not dazzle quite yet, especially for those eagerly awaiting an explanation of time and space. Rest assured, it’s in there—we’re not quite done yet. What we do possess is a pivotal part of the grand pattern: the evolution of points, rays, and vectors in major and minor variations. Fundamentally, that’s all we need plus one insight understanding. Yes, the 18 objects seem disjointed now, but fret not. The Eureka moment comes when we shine light on it.
In the grand tapestry of the universe, what researchers can agree on is that everything is interconnected by Electromagnetism. Now, while enigmatic entities like Dark Matter and Dark Energy linger on the fringes of this understanding, aligning those too with the geometric primer and electromagnetism, raises the stakes.
